Bringing Google's Authentic Motion to iOS via Bézier Curve Fitting
During this year's I/O conference Google showed that it cares about the design. While browsing through its website, I noticed an interesting approach to animations called Authentic Motion. Google's designers created a new animation curve called Swift Out and described it as:
Motion with swift acceleration and gentle deceleration feels natural and delightful.
There's also a short demo of it:
I thought it would be nice to have this animation curve on iOS and proceeded to reverse-engineer it.
Timing functions
I won't be describing pre-existing timing functions from scratch, because this topic has already been extensively covered, e.g. by Robert Böhnke in Animations Explained. What's important to us, is that CAMediaTimingFunction can be created from a Bézier curve with a class method + functionWithControlPoints::::. This method implicitly assumes that endpoints are located at (0.0,0.0) and (1.0,1.0), because:
CAMediaTimingFunctionrepresents one segment of a function that defines the pacing of an animation as a timing curve. The function maps an input time normalized to the range [0,1] to an output time also in the range [0,1].
We can set two control points, though, which means we're able to use any cubic Bézier curve with it. Sidenote: a Bézier path—commonly used in iOS and Mac development—is a more general object; it can be combined from many linked Bézier curves.
Fitting Bezier Curve
Interpolating a cubic Bézier curve analytically, such that it passes through four data points isn't that hard. The problem is that infinitely many curves can pass through these points, depending on chosen x coordinates of the control points. We would get a different curve with x1 = 1/3, x2 = 2/3 than with x1 = 3/8, x2 = 3/4, but they both would pass through the data points.
Finding a control points of a cubic curve based on more than four data points is harder, because it leads to a non-linear optimization problem. It means that to get a curve similar to Google's we have to use an approximate numerical algorithm1. After some research I'd found that Philip J. Schneider's algorithm described in An algorithm for automatically fitting digitized curves is a popular solution to this problem. Then, I found an Objective-C implementation of it created by Andy Finnell. I was ready to do the fitting.
I extracted 32 data points2 (x and y pairs) from this image:
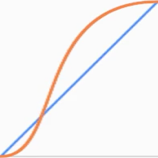
and, based on Andy's code, created a simple command line app that reads points from a file and finds a cubic curve based on them. The fit wasn't perfect, but nonetheless, I'm quite happy with the result:

The control points found by the algorithm can be translated directly into an Objective-C method:
+ (CAMediaTimingFunction *)swiftOut
{
CGPoint controlPoint1 = CGPointMake(0.4027, 0.0);
CGPoint controlPoint2 = CGPointMake(0.2256, 1.0);
return [self functionWithControlPoints:controlPoint1.x :controlPoint1.y :controlPoint2.x :controlPoint2.y];
}
To make sure it's working correctly I made a sample app (see it on GitHub), which uses this new animation curve:
Afterthoughts and Verification
After some more digging I found out that this curve is already used in Chromium. It's based on control points: (0.4, 0.0) and (0.2, 1.0), so the fitted curve is close to it. Here is a history of its names and annotations from the Chromium repo:
Mar 12 2014: FAST_OUT_SLOW_IN // Variant of EASE_IN_OUT which should be used in most cases.
Feb 10 2014: EASE_IN_OUT_2 // Variant of EASE_IN_OUT which starts out faster than EASE_IN_OUT but ends slower than EASE_IN_OUT.
Feb 05 2014: EASE_OUT_BEZIER, // Variant of EASE_OUT that starts and ends slower.
UPDATE (15-07-2014): I published a follow-up post in which I show how to use the derived curve to implement a hamburger button animation.
